数学初三上 第二十六章 二次函数
26.2 特殊二次函数的图像 第一课时（1）
1、选择题
1. 关于
和
的图像的说法：①它们都是轴对称图形；②它们的顶点相同，对称轴也相同；③它们都是抛物线；④两个函数图像关于x轴对称。这类说法正确的有
（ ）
A． 4个 B. 3个 C. 2个 D. 1个
2. 关于二次函数
，下列说法正确的是 （ ）
A．若a>0，则y随x的增大而增大 B. 若a>0，则y随x的增大而减小
C. 若a<0，则y有最大值 D. 若a>0，则y有最大值
3. 关于二次函数
与
的图像，则下列结论不正确的是 （ ）
A． 这两个函数图像具备相同的对称轴 B. 这两个函数图像的开口方向相反
C. 这两个函数图像的开口大小相同 D. 这两个函数图像具备相同的顶点
4. 已知点（-1，y1）、（0，y2）、（1，y3）均在函数的图像上，则y1、y2、y3的大小关系是 （ ）
A．y1>y2=y3 B. y2> y1 =y3 C. y1=y2=y3 D. y2< y1=y3
5. 将二次函数的二次项系数变为原来的2倍，得到新的图像的二次函数表达式是 （ ）
A．
B. C. 
D. 
6. 二次函数的二次项系数缩小为原来的
，得到新的图像的二次函数表达式是 （ ）
A．
B. C. 
D.
2、填空题
7．一般二次函数
的图像是__________。
8. 抛物线的对称轴是_________________，顶点坐标是_________________，图象开口向_________________.
9. 二次函数
的图像是抛物线，则m的取值范围是__________。
10. 已知
是二次函数，则k需要满足的条件是__________。
11. 函数
的图像是抛物线，其开口方向是__________。
12. 若抛物线
开口向下，则m=__________。
13. 抛物线的对称轴是_________________，顶点坐标是_________________，图象开口向_________________.
14. 抛物线，当
时，y随x的增大而__________；当
时，y随x的增大而__________。
3、解答卷
15. 用列表法在同一个坐标系内画出和
的图像，并说明它们的相同点和不同的地方。
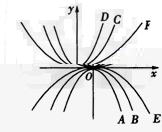
16. （1）请将图中图像的编号填入对应的函数后面的空格内：__________，__________，
__________，__________，__________，__________。
（2）二次函数的图像的开口的大小与a有什么样的关系？请写出你的结论。
17、已知关于x的二次函数
，当m为什么值时，图像开口向下？当m为什么值时，图像开口向上？
18. 已知直线
与抛物线相交于两点，求示数m的取值范围。
19. 函数
与直线相交于点（1，b）
（1）求a和b的值；
（2）求抛物线
的分析式，并求顶点坐标和对称轴。
（3）求抛物线与直线y=2的两交点及与顶点构成的三角形的面积。
20. 如图甲是某段河床横截面的示意图，查阅该河段的水文资料，得到下表中的数据：
x/m | 5 | 10 | 20 | 30 | 40 | 50 |
y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
（1）请你以上表中的各对数据（x，y）作为点的坐标，尝试在图2所示的坐标系中画出y关于x的函数图象；
（2）①填写下表：
x | 5 | 10 | 20 | 30 | 40 | 50 |
|
|
|
|
|
|
|
②依据所填表中数据呈现的规律，猜想出用x表示y的二次函数的表达式：__________；
（3）当水面宽度为36米时，一艘吃水深度（船底部到水面的距离）为1.8米的货船能否在这个河段安全通过？为何？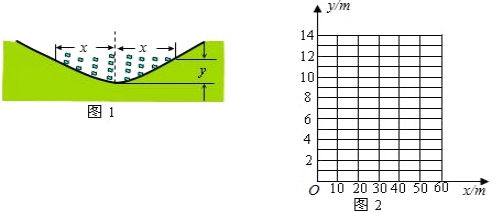
21. 已知抛物线经过点（-2，-8）
（1）求a的值.
（2）判断点B是不是在此抛物线上.
（3）求出此抛物线上纵坐标为-6的点的坐标.
数学初三上 第二十六章 二次函数
26.2 特殊二次函数的图像 第一课时（1）
参考答案
1. A 2. C 3. C 4. D 5. A 6. B
7. 抛物线
8. y轴（直线x=0） 下
9.
10. 
且
11. 向上
12. -3
13. y轴（直线x=0） 下
14. 增大 减小
15.
| 相同点 | 不同的地方 | |||||
图像形状 | 开口大小 | 顶点 | 对称轴 | 开口方向 | 增减性 | ||
x<0 | x>0 | ||||||
| 抛物线 | 相同 | （0，0） | x=0 | 向下 | y随x的增大而增大 | y随x的增大而减小 |
| 抛物线 | 相同 | （0，0） | x=0 | 向上 | y随x的增大而减小 | y随x的增大而增大 |
16. （1）A B E D C F
（2）
越大，开口越小；越小，开口越大
17. 当m<2时，图像开口向下，当m>2时，图像开口向上
18. 
, 提示：把代人，由
可得
19. （1）a=1, b=1
（2）抛物线的分析式：，顶点坐标（0，0），对称轴x=0
（3）
20. （1）图象如下图所示；（2分）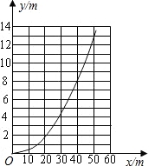
（2）①填表正确；（5分）
x | 5 | 10 | 20 | 30 | 40 | 50 |
| 200 | 200 | 200 | 200 | 200 | 200 |
②∵由上表可知
=200，
∴
（6分）
（3）当水面宽度为36m时，相应的x=18，
则=1.62，
此时该河段的最大水深为1.62m（8分）
由于货船吃水深为1.8m，而1.62m＜1.8m，
所以当水面宽度为36m时，该货船不可以通过这个河段．（10分）
23. （1）a=-2
（2）B 不在此抛物线上
（3）（
），（
）
